Бесконечномерные интегрируемые системы математической физики

Одно из основных направлений работы лаборатории - исследование бездисперсионных интегрируемых систем, называемых также системами гидродинамического типа. В 1984 году Б.А.Дубровиным и С.П.Новиковым [1] был построен гамильтонов формализм систем Уизема, причем оказалось, что скобки Пуассона такого типа порождаются плоскими псевдоримановыми метриками на многообразиях, в которых поля принимают значения. При этом в естественно возникающих координатах метрика не постоянна, и приведение скобки к каноническому виду - достаточно нетривиальная задача. Механизм интегрирования таких систем (обощенный метод годографа) был найден С.П.Царевым [2].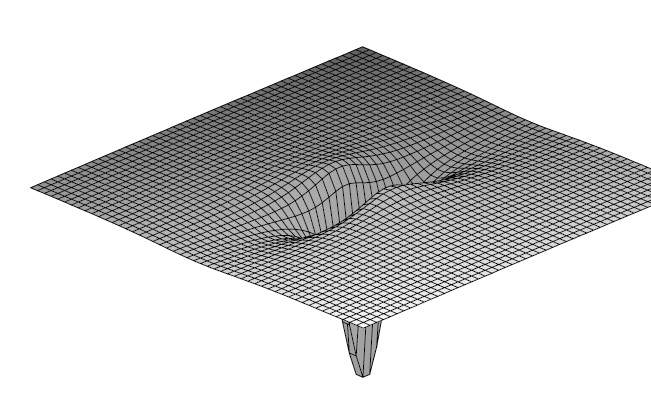

Системы с малой дисперсией естественно рассматривать как возмущения систем с нулевой дисперсией. Б.А.Дубровиным и его учениками - Ли и Жангом [3,4] был исследован вопрос о приведении бигамильтоновых возмущений таких систем к каноническому виду при помощи обобщенных преобразований Миуры, когда замена полевых переменных представляет собой ряд по малому параметру, причем в главном порядке преобразование сводится к невырожденной замене координат, а производные появляются лишь в следующих порядках. Такие преобразования обратимы, и оказывается, что в ряде примеров все возмущения оказываются тривиальными. Так, например, на уровне рядов, уравнение Кортевега-де Фриза с малой дисперсией оказывается эквивалентным уравнению Хопфа. В настоящее время иссследуется ситуация с другими классами уравнений.

С аналитической точки зрения, системы с нулевой дисперсией служат хорошим приближением для систем с малой дисперсией до тех пор, пока не начинают образовываться ударные волны. При этом в области образования ударных волн сколь угодно малая дисперсия становится существенной, и в разных областях решение начинает описываться уравнениями Уизема с различным числом зон [5] (Гуревич-Питаевский, Новиков, Дубровин, Авилов). В работах Б.А.Дубровина, Т.Гравы и К.Клейна [6] было высказано предположение, что в точке образовния ударной волны также имеет место некоторое универсальное поведение, причем для фокусирующего нелинейного уравнения Шредингера в качестве модельного выступает специальное решение уравнения Пенлеве-I (tritronquee solution). 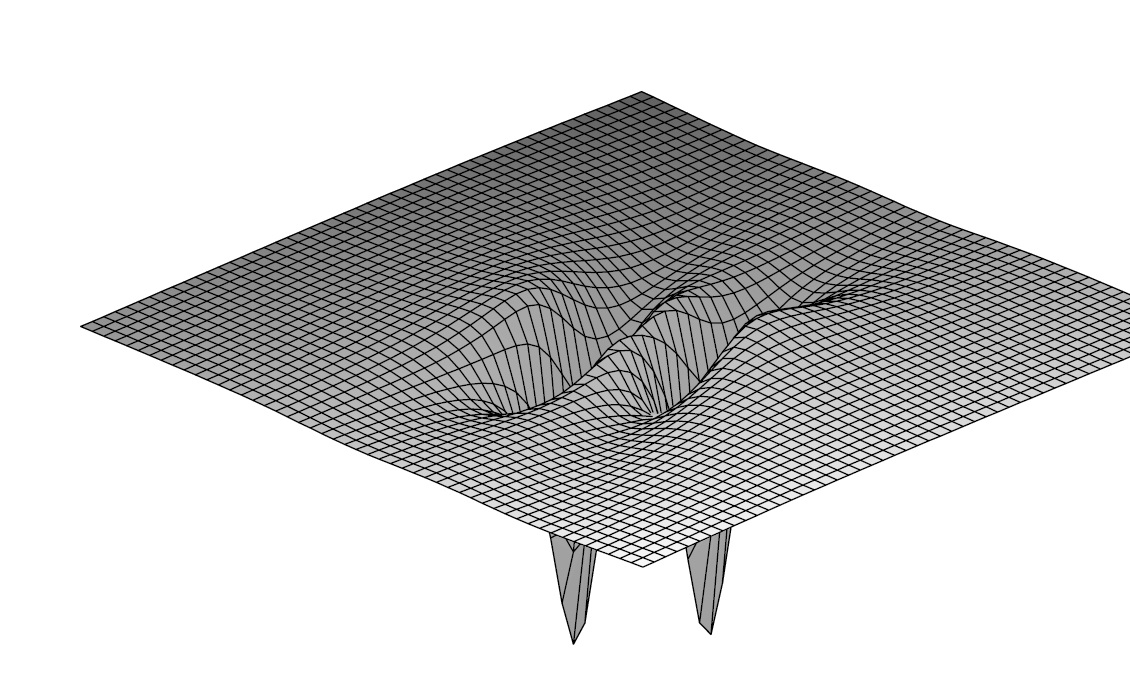Данное направление исследований требует как применения тонких аналитических методов, так и крайне надежных вычислительных схем, сохраняющих стабильность в присуствии существенной численной неустойчивости.

Еще одно направление исследований - установление связей систем гидродинамического типа с топологическими теориями поля, уравнениями ассоциативности, инвариантами Громова-Виттена, приложения теории Фробениусовых многообразий.

В работах Манакова и Сантини был предложен новый подход к построению решений бездисперсионных интегрируемых систем, основанный на нелинейной задаче Римана. Однако вопрос о том, насколько общие классы решений при этом получаются, пока остается открытым. Исследование прямого преобразования рассеяния для таких уравнений начато в недавней работе Гриневича и Сантини [7], при этом показано, что для гамильтонова векторного поля, входящего в пару Лакса бездисперсионного уравнения Кадомцева-Петрвиашвили (уравнения Хохлова-Заболоцкой) существуют голоморфные по спектральному параметру вне некоторой полосы нулевые собственные функции.

Одна из важнейших интегрируемых моделей - двумерный оператор Шредингера, рассматриваемый при фиксированной энергии. Интегрируемость этой задачи была была установлена Дубровиным, Кричевером и Новиковым [8] в 1976 году. Задача выделения чисто электрических операторов (операторов с нулевым магнитным полем) была решена Веселовым и Новиковым в 1983 году для периодических (конечнозонных при одном уровне энергии) операторов. Другой важный случай - теория основного состояния периодических чисто магнитных операторов была развита Б.А.Дубровиным и С.П.Новиковым в 1980 году [9], но до недавнего времени не удавалось сопоставить эти два подхода, пока П.Г.Гриневичем, А.Е.Мироновым и С.П.Новиковым в 2010 году не была найдена редукция на конечнозонные спектральные данные, отвечающая нулевому электрическому полю [10, 11]. Оказалось, что комплексное продолжение кривой Ферми энергии основного состояния распадается на две компоненты с соотношениями на волновые функции в точках пересечения, что позволило найти новые точно решаемые случаи, включая периодические поля с ненулевым целочисленным потоком через элементарную ячейку.

Отдельный интерес представляет задача о построении интегрируемых при одной энергии дискретизаций двумерного оператора Шредингера. Гиперболическая дискретизация была найдена в 1985 году И.М.Кричевером [12], эллиптическая дискретизация была найдена П.Г.Гриневичем, А.Доливой, М.Нишпорским и П.М.Сантини в 2007 году [13]. Последняя была использована при решении задачи об описании примианов кривых с инволюциями без неподвижных точек в работе И.М.Кричевера и С.Грушевского [14], где, в частности, были построены общие конечнозонные решения для данных операторов. В настоящее время преобразование рассеяния для операторов с локализованнымы потенциалами изучается П.Бурангуловым, функции Грина для периодических конечнозонных оператров исследуются Б.Василевским.

В лаборатории также ведется работа по исследованию обратной задачи рассеяния для двумерного оператора Шредингера при фиксированной энергии. До сих пор остается открытым вопрос о правильной постановке задачи рассеяния для случая, когда фаддевские решения имеют особенности при данной энергии и комплексном импульсе. Одна из трудностей данной задачи - отсутствие модельных примеров. В работе П.Г.Гриневича и Р.Г.Новикова [15] разобрана точно решаемая модель - рассеяние на двумерном точечном потенциале, для которой особые контура и поведение волновых функций вблизи них описываются простыми явными формулами. Этот пример является двумерным аналогом трехмерного точечного потенциала, исследованного в классических работах Я.Б.Зельдовича [16], Ф.А. Березина и Л.Д.Фаддеева [17].

Литература:

1. Б.А. Дубровин, С.П. Новиков, О скобках Пуассона гидродинамического типа, Докл. Акад. наук СССР, 279(1984) вып. 2, 294-297.
2. С.П. Царев, О скобках Пуассона и одномерных гамильтоновых системах гидродинамического типа, Докл. Акад. Наук СССР, 282(1985), вып. 3, 534-537.
3. B.A. Dubrovin, Si-Qi Liu, Youjin Zhang, On Hamiltonian perturbations of hyperbolic systems of conservation laws I: quasi-triviality of bi-hamiltonian perturbations. Comm. in Pure Appl. Math. 59 (2006), 559-615.
4. B.A.Dubrovin, On Hamiltonian perturbations of hyperbolic systems of conservation laws II: universality of critical behaviour, Comm. Math. Phys. 267 (2006), 117-139.
5. В.Е. Захаров, С.В. Манаков, С.П. Новиков, Л.П. Питаевский, Теория солитонов. Метод обратной задачи, М.: Наука, 1980 - 320 с.
6. B.A. Dubrovin, T. Grava and C. Klein, On universality of critical behaviour in the focusing nonlinear Schroedinger equation, elliptic umbilic catastrophe and the tritronquee solution to the Painleve'-I equation, J. Nonlinear Sci. 19 (2009), 57-94.
7. P.G. Grinevich, P.M. Santini, Holomorphic eigenfunctions of the vector field associated with the dispersionless Kadomtsev-Petviashvili equation arXiv:1111.4446.
8. Б.А. Дубровин, И.М. Кричевер, С.П. Новиков, Уравнение Шредингера в периодическом поле и римановы поверхности, Докл. Акад. наук СССР, 229 (1976) вып. 1, 15-18.
9. Б.А. Дубровин, С.П. Новиков, Основные состояния в периодическом поле. Магнито-блоховские функции и векторные расслоения, Докл. Акад. наук СССР, 253 (1980) вып. 6, 1293-1297.
10. П.Г. Гриневич, А.Е. Миронов, С.П. Новиков, Двумерный оператор Паули в магнитном поле, Физика низких температур, 37 (2011), N 9-10, 1040-1045.
11. П.Г. Гриневич, А.Е. Миронов, С.П. Новиков, О нулевом уровне чисто магнитного двумерного нерелятивистского оператора Паули для частиц со спином 1/2. Теоретическая и математическая физика, 164 (2010), N 3, 333-353.
12. И.М. Кричевер, Двумерные периодические разностные операторы и алгебраическая геометрия, Докл. Акад. наук СССР, 285 (1985), вып. 1, 31-36.
13. A. Doliwa, P.G. Grinevich, M. Nieszporski, P.M. Santini, Integrable lattices and their sub-lattices: from the discrete Moutard (discrete Cauchy-Riemann) 4-point equation to the self-adjoint 5-point scheme. Journal of Mathematical Physics, 48 (2007), N 1. Paper 013513, 28 pages.
14. S. Grushevsky, I. Krichever, Integrable discrete Schroedinger equations and a characterization of Prym varieties by a pair of quadrisecants. Duke Math. J., 152 (2010), 317-371; arXiv:0705.2829.
15. P.G. Grinevich, R.G. Novikov, Faddeev eigenfunctions for point potentials in two dimensions arXiv:1110.3157.
16. Я.Б. Зельдович, Рассеяние сингулярным потенциалом в теории возмущений и в импульсном представлении, ЖЭТФ 38 (1960), 819.
17. Ф.А. Березин, Л.Д. Фаддеев, Замечание об уравнении Шредингера с сингулярным потенциалом, Докл. Акад. наук СССР, 137 (1961), вып. 5, 1011-1014.